Pourquoi le bouton “se souvenir de moi” n'est-il pas toujours cliquable ?
↪Pour que la case à cocher “Permanent” soit accessible dans le menu de connexion, vous devez avoir accepté les cookies. Si vous les refusez, il n'est pas possible de mémoriser vos informations de connexion. La seule possibilité de les mémoriser c'est dans un cookie. Vous trouverez plus d'information sur le fonctionnement des cookies sur la page des mentions légales, dont un lien vous permettant de supprimer votre choix précédent.
Pourquoi les non n'apparaissent-ils pas toujours quand je mets un oui ?
↪Parce que cela peut pénaliser les joueurs qui jouent en mode compétition. Les plus forts font la différence en ne perdant pas de temps à positionner les non. Par contre, si vous jouez en mode Zen, si le oui se trouve dans le groupe de lignes du haut, la valeur est également ajoutée dans le tableau des résultats.
Et si vous avez coché « avec remplissage automatique ? » dans les paramètres de votre compte, en mode Zen, dès que vous positionnez un oui, les non autour sont automatiquement complétés… Si vous effacez votre oui, les non qui avaient été ajoutés automatiquement, sont effacés. Par contre la valeur n'est pas supprimée dans le tableau de la solution. Attention : il n'y a pas de contrôle.
Pourquoi n'y a-t-il pas plus d'intégrammes sur le site ?
↪Tout simplement parce que cela prend beaucoup de temps de les créer, les tester, et d'ajouter de l'aide… MAIS vous pouvez m'aider en en créant vous-même. Il vous suffit ensuite de me les envoyer. Vous pouvez me contacter pour connaître la marche à suivre.
Les caractères et les grilles sont trop petits !
Si les caractères étaient plus gros (donc les tableaux plus grands) ça aiderait mes vieux yeux.
↪J'étudie actuellement une solution pour agrandir, ou rétrécir, les grilles, cela devrait arriver dans quelque temps. D'ici là, vous avez la possibilité d'utiliser la fonction zoom de votre navigateur internet. Vous pouvez y accéder par le menu du navigateur, ou sur PC avec la touche CTRL et la molette de votre souris.
La vérification de la solution devrait couper le chrono !
↪En réalité, elle la coupe… sans la couper ! Je m'explique : quand vous cliquez sur le bouton de vérification de la solution, le temps est conservé, et c'est celui-ci qui est utilisé, et ré-affiché, si votre solution est bonne. Si elle n'est pas bonne, le chrono continue.
Pourquoi j'ai un message “Quitter le site web ?” ?
Quand je clique sur un bouton en haut ou en bas de la page de jeu, j'ai une question “Quitter le site web ? Les modifications que vous avez apportées ne seront peut-être pas enregistrées.”.
↪C'est parce que vous avez une partie en cours. C'est une précaution pour ne pas perdre votre avancée sur cet intégramme. Cela ne veut pas dire que vous allez quitter intégrammes.fr, juste que vous allez quitter la page de jeu. Le message n'est pas très explicite, mais il est imposé par les navigateurs. Si vous avez résolu cet intégramme, avec succès, et que vous cliquez sur l'un des boutons en haut ou en bas de page, vous n'aurez plus cette question.
Peut-on jouer sur un portable ou une tablette ?
↪Oui ! Le site est prévu pour avoir un rendu agréable quelle que soit la taille de l'écran (appelé mode responsive). La page de jeu s'adapte également à la taille de votre écran en changeant la taille des icônes et en proposant automatiquement l'affichage Compact ou Smart. Vous pouvez changer de mode à tout moment grâce à l'icône. Le mode Smart est plus adapté aux ordinateurs, car le survol d'une case avec la souris met en avant le titre de la colonne. Un mode Smart plus adapté aux tablettes et téléphones est en cours de préparation. Par ailleurs, afficher un intégramme de taille importante sur un petit écran est complexe : soit il faut scroller, soit il faut zoomer/dézoomer, mais si vous avez des suggestions, n'hésitez surtout pas à me contacter.
Je joue beaucoup sur tablette, les intitulés des colonnes sont souvent tronqués !
↪Depuis, j'ai fait des efforts sur la longueur des intitulés, et les efforts continuent… De plus, j'ai adapté le mode Compact pour permettre un meilleur affichage des intitulés de grandes tailles, mais qui reste raisonnable.
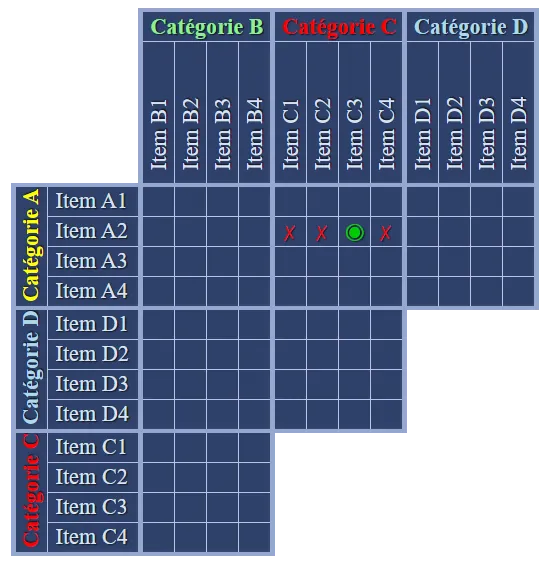
Je ne comprends pas à quoi correspondent toutes les cases qui clignotent !
↪Quand vous demandez de l'aide sur une énigme, avec la tête du professeur, certaines cases peuvent clignoter en retour :
- Quand une case clignote de cette couleur, cela signifie que cette case est en erreur, et qu'il n'est pas possible de vous proposer une aide.
- Quand il n'y a pas d'erreur, l'appel de l'aide ajoute une réponse oui ou non qui clignote. En passant la souris au-dessus de la tête du professeur, vous saurez comment cette aide a été calculée.
- Dans certains cas, l'aide que vous obtenez dépend de la valeur d'autres cases. Celles-ci sont signalées par un cercle qui clignote.
Vous n'avez pas trouvé ici de réponses à votre question ? Vous les trouverez peut-être sur la page d'aide, vous pouvez aussi me contacter directement.
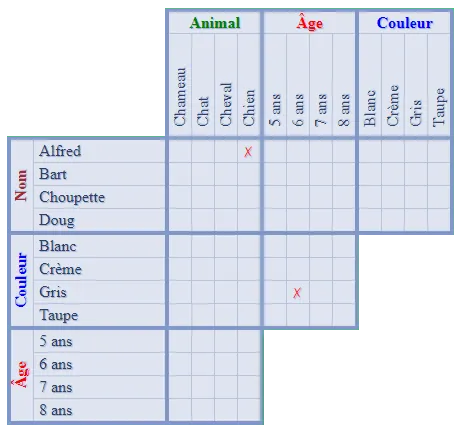
 de l'ensemble des groupes (appelés aussi catégories) et de leurs sujets (appelés aussi éléments) rangés sur le côté gauche et le haut d'une grille. Cette grille offre toutes les correspondances possibles entre deux sujets quelconques de deux groupes différents. La résolution du problème se fait en écrivant un non lorsque la correspondance est fausse, ou un oui lorsque la correspondance est vraie.
de l'ensemble des groupes (appelés aussi catégories) et de leurs sujets (appelés aussi éléments) rangés sur le côté gauche et le haut d'une grille. Cette grille offre toutes les correspondances possibles entre deux sujets quelconques de deux groupes différents. La résolution du problème se fait en écrivant un non lorsque la correspondance est fausse, ou un oui lorsque la correspondance est vraie. d'une solution unique (à trouver). Pour cela, une fois que la grille est remplie, il suffit de reporter dans le formulaire de réponse les valeurs correspondantes aux oui des groupes du haut de la grille.
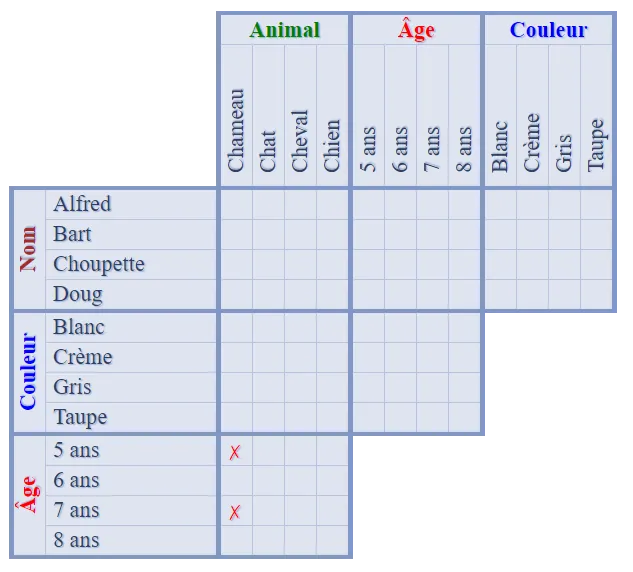
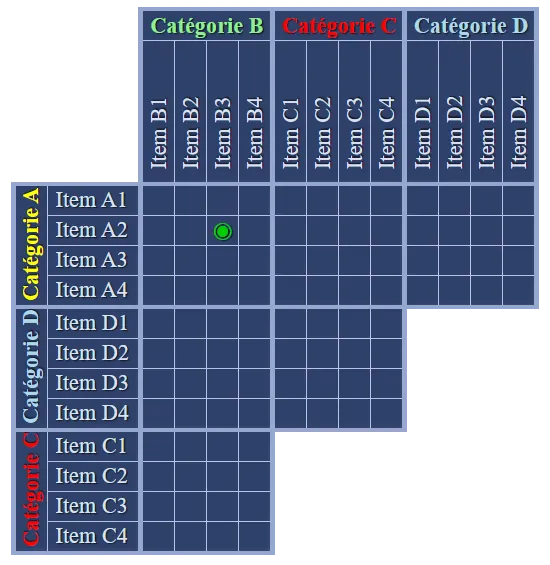
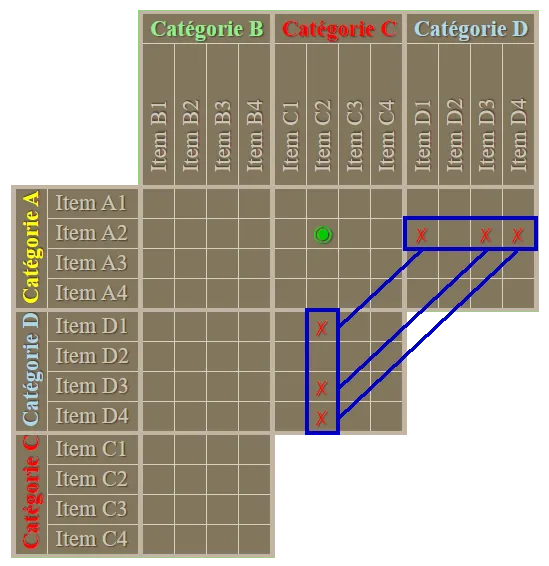
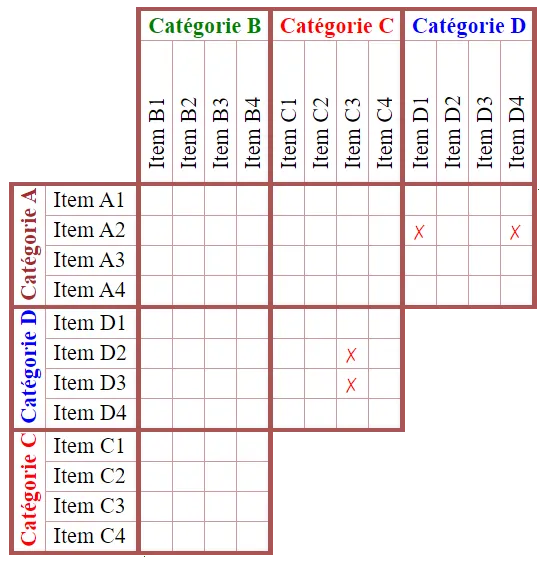
d'une solution unique (à trouver). Pour cela, une fois que la grille est remplie, il suffit de reporter dans le formulaire de réponse les valeurs correspondantes aux oui des groupes du haut de la grille. Que nous apprend le premier indice : Le garçon châtain a pris une glace dragibus, nous pouvons donc mettre un
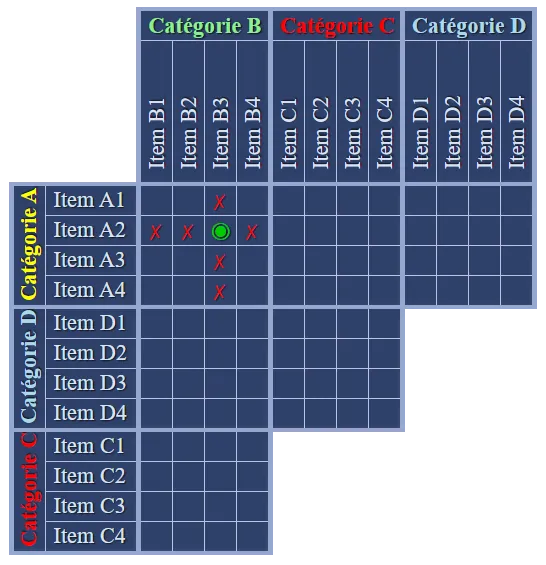
Que nous apprend le premier indice : Le garçon châtain a pris une glace dragibus, nous pouvons donc mettre un 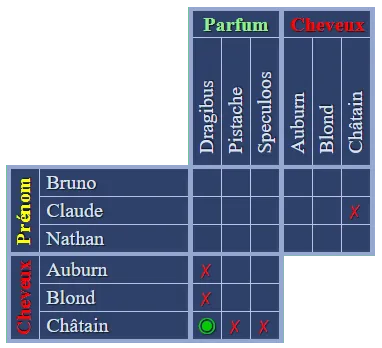 Que nous enseigne le
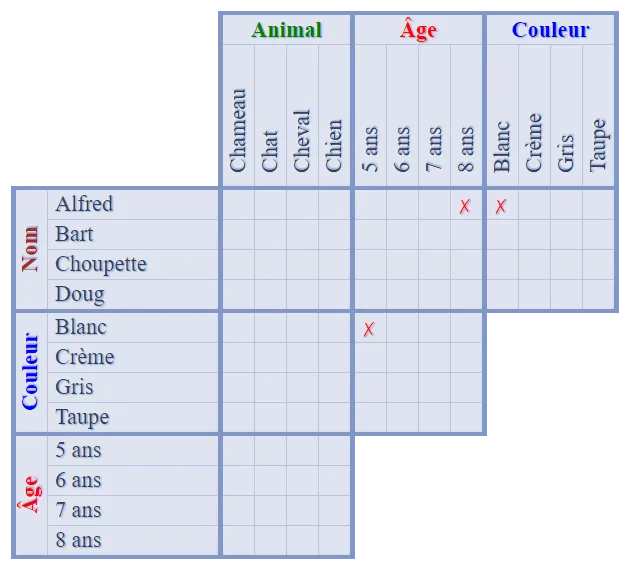
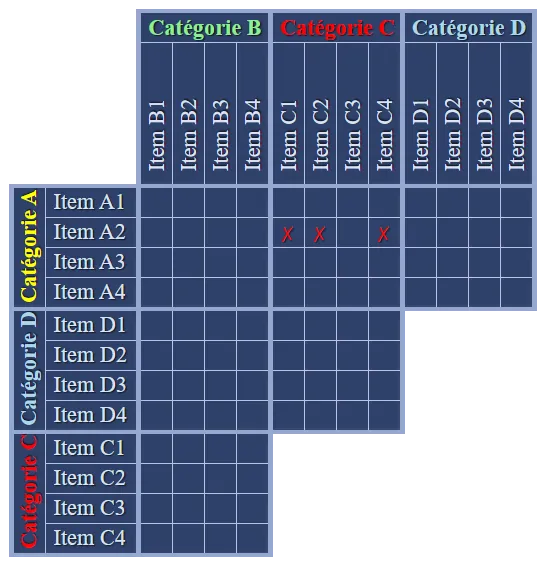
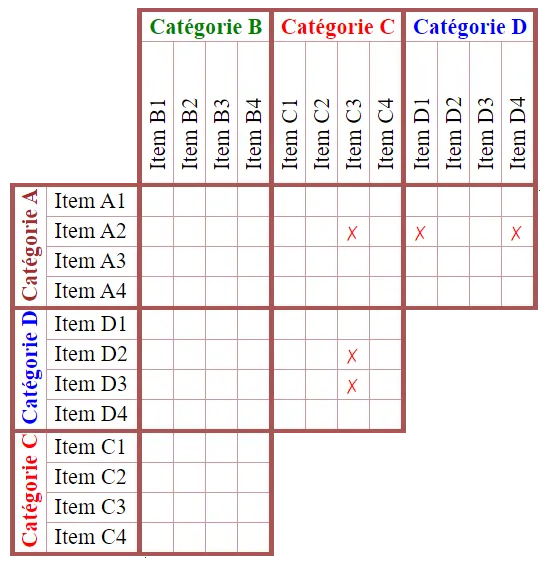
Que nous enseigne le  Que nous apprend le deuxième indice : Nathan est blond, nous pouvons donc mettre un
Que nous apprend le deuxième indice : Nathan est blond, nous pouvons donc mettre un 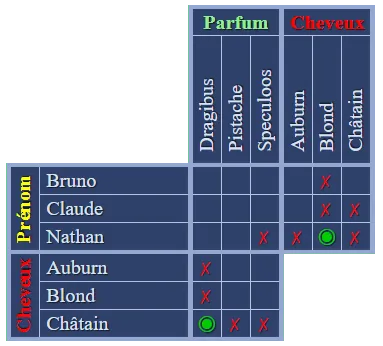 Utilisons à nouveau le
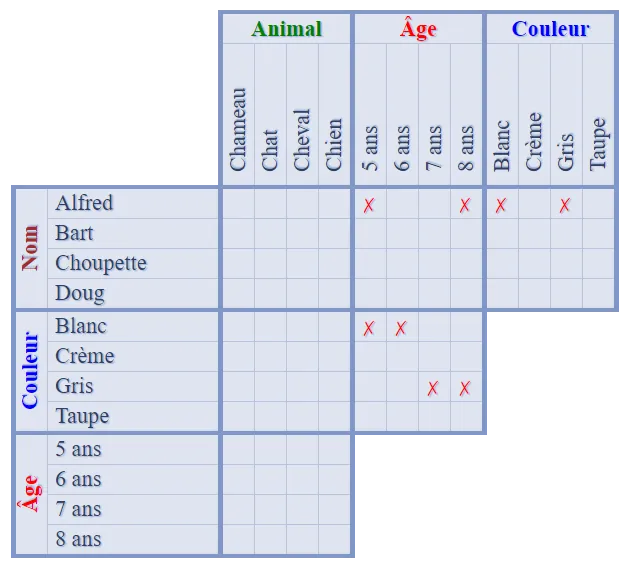
Utilisons à nouveau le  Que nous apprend le
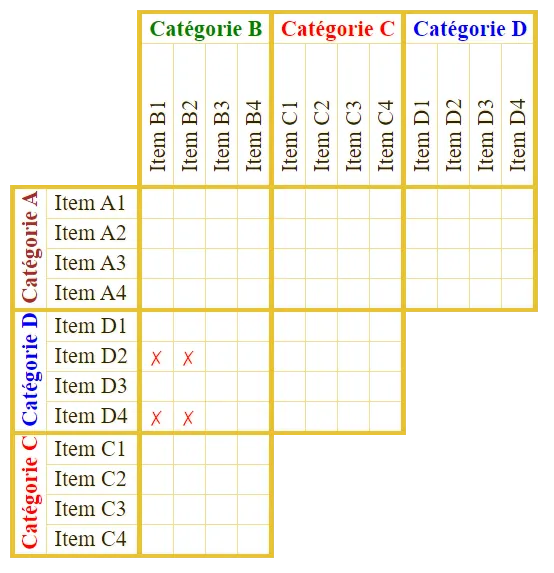
Que nous apprend le 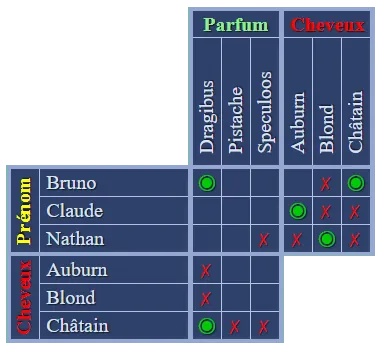 Que nous apprend la
Que nous apprend la 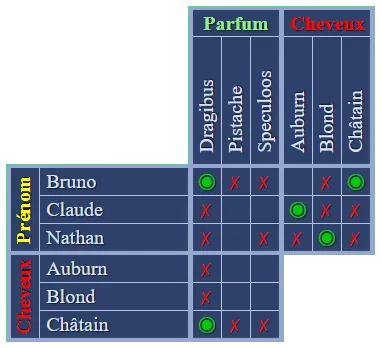 Utilisons à nouveau le
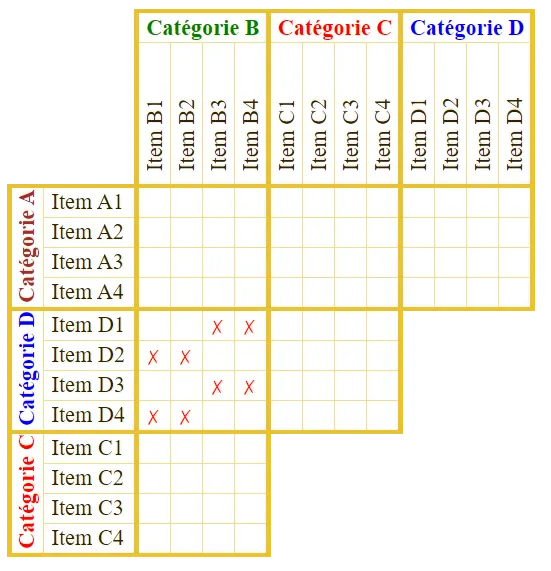
Utilisons à nouveau le 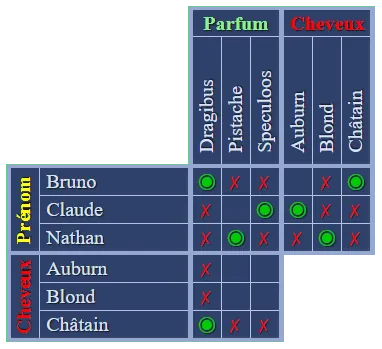 Enfin, appliquons une dernière fois le
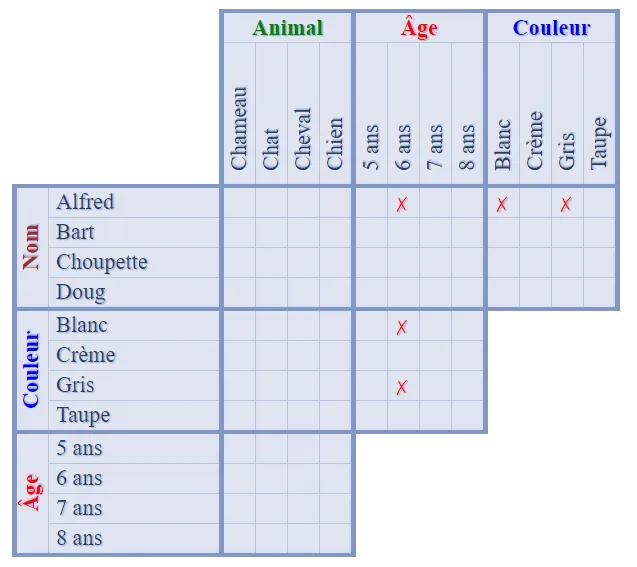
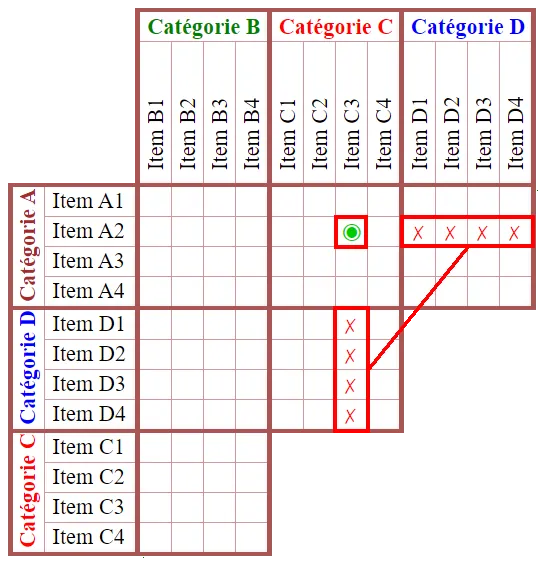
Enfin, appliquons une dernière fois le  Vous pouvez compléter les cases vides restantes, ou reporter directement les
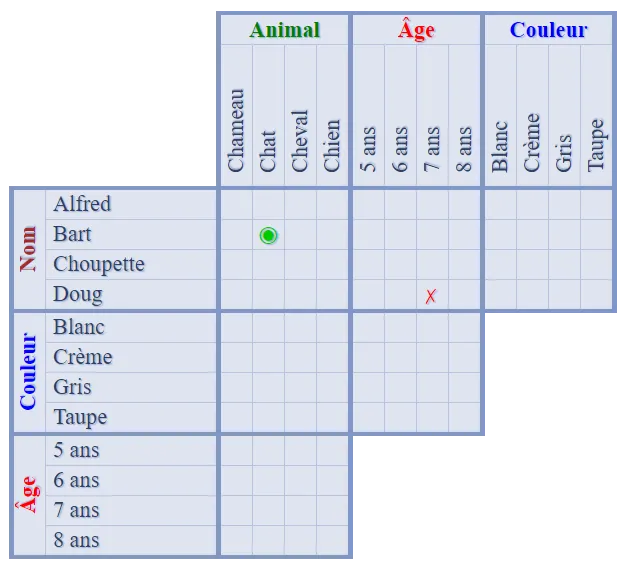
Vous pouvez compléter les cases vides restantes, ou reporter directement les 
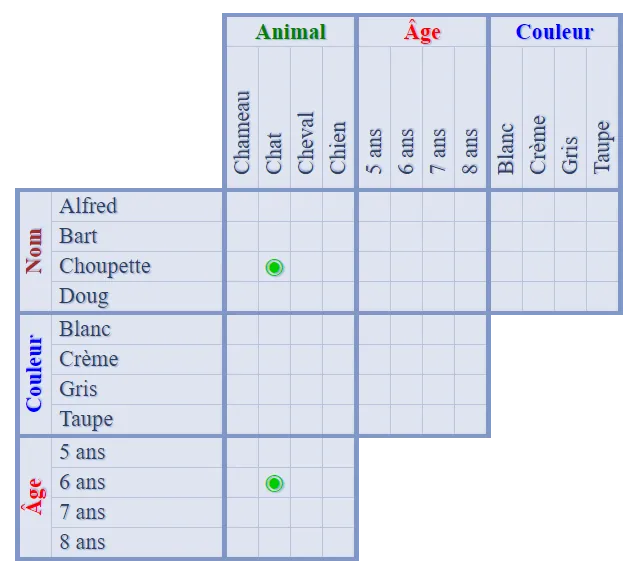

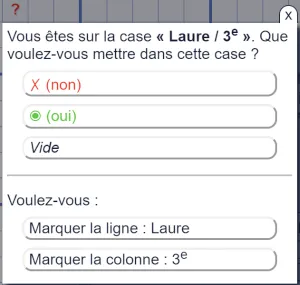 Ce mode peut vous aider si vous avez du mal à cliquer sur une case précise (tremblements, cases petites sur un téléphone…) ou si vous ne voyez par l'intégralité de la grille, notamment sur téléphone. La fenêtre d'aide à la saisie vous évite de cocher une case par erreur, en l'effleurant simplement. Elle vous précise où vous êtes exactement sur la grille et vous propose les différentes possibilités pour remplir la case. Elle vous permet également de mettre en évidence la ligne ou la colonne correspondante. Ceci peut être très utile quand vous jouez sur de grandes grilles sur téléphone et que vous ne voyez pas les entêtes.
Ce mode peut vous aider si vous avez du mal à cliquer sur une case précise (tremblements, cases petites sur un téléphone…) ou si vous ne voyez par l'intégralité de la grille, notamment sur téléphone. La fenêtre d'aide à la saisie vous évite de cocher une case par erreur, en l'effleurant simplement. Elle vous précise où vous êtes exactement sur la grille et vous propose les différentes possibilités pour remplir la case. Elle vous permet également de mettre en évidence la ligne ou la colonne correspondante. Ceci peut être très utile quand vous jouez sur de grandes grilles sur téléphone et que vous ne voyez pas les entêtes.