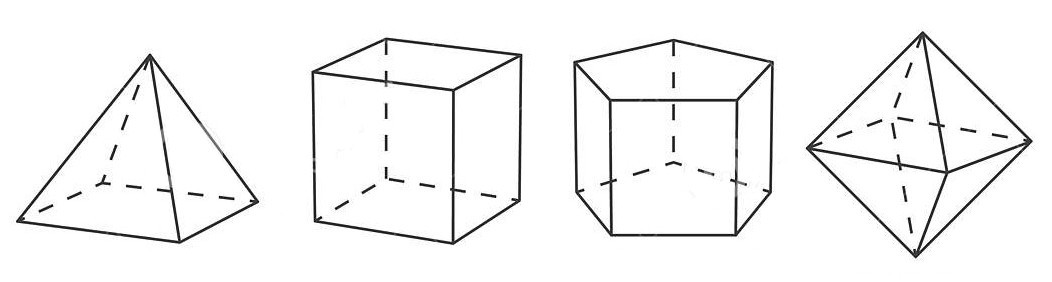
Serez-vous aussi doué qu’Euler pour résoudre ce problème ?
L’exercice consiste à analyser différentes figures géométriques solides pour déterminer leurs caractéristiques fondamentales : le nom, le nombre de faces et le nombre de sommets. Ces éléments sont essentiels pour décrire un solide dans le cadre de la géométrie topologique.
Pour trouver la solution de ce problème, vous pouvez utiliser les indices, le dessin des solides ainsi que la relation d’Euler. Cette formule permet de vérifier la cohérence des résultats obtenus et de mieux comprendre les propriétés géométriques des solides étudiés.
Rappel : La relation d’Euler pour les polyèdres convexe stipule que la somme du nombre de sommets et du nombre de faces, moins le nombre d’arêtes, est égale à 2.
Note : Tout est véridique dans cet intégramme, mais ce n’est pas la peine de vous précipiter sur votre encyclopédie préférée ou sur internet, vous devriez facilement trouver la solution à partir des indices.
Intégramme de difficulté 2/10 et de taille 4x4
230 - Math : Euler et les solides |
Nom |
Faces |
Sommets | ||||||||||
Prisme |
Cube |
Pyramide |
Octaèdre |
5 |
6 |
7 |
8 |
5 |
6 |
8 |
10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Solide |
A | ||||||||||||
| B | |||||||||||||
| C | |||||||||||||
| D | |||||||||||||
Sommets |
5 | ||||||||||||
| 6 | |||||||||||||
| 8 | |||||||||||||
| 10 | |||||||||||||
Faces |
5 | ||||||||||||
| 6 | |||||||||||||
| 7 | |||||||||||||
| 8 | |||||||||||||
Le Top 10 des meilleurs scores n'est pas disponible pour les intégrammes dont les données sont réelles ou ne changent pas entre chaque partie.
Vos temps sont quand même enregistrés, vous pouvez les retrouver dans votre historique. Votre objectif principal est probablement de vous améliorer, pas de vous comparer avec des joueurs qui peuvent tricher sur des grilles toujours identiques ou dont les solutions sont publiques.
